Let's continue!
Today is mainly learning about "Decision boundary", "Cost function of logistic regresion", "Logistic loss" and "Gradient Descent Implementation for logistic regression".
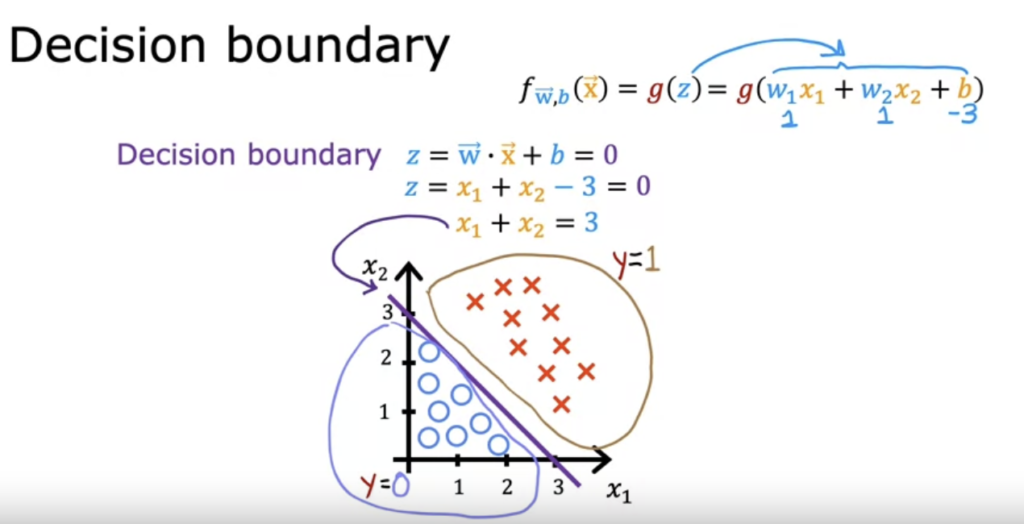
We found out the "Decision boundary" is when z equals to 0 in the sigmod function.
Because at this moment, its value will be just at neutral position.
Andrew gave an example with two variables, x1 + x2 - 3 (w1 = w2 = 1) the decision bounday is the line of x1 + x2 = 3.
I want to say "Cost function for logistic regression" is the most hard in week 3 so far I've seen.
I haven't quite figured out why the square error cost function not applicable and where the loss function came from.
I have to re-watch the videos again.
The lab is also useful.
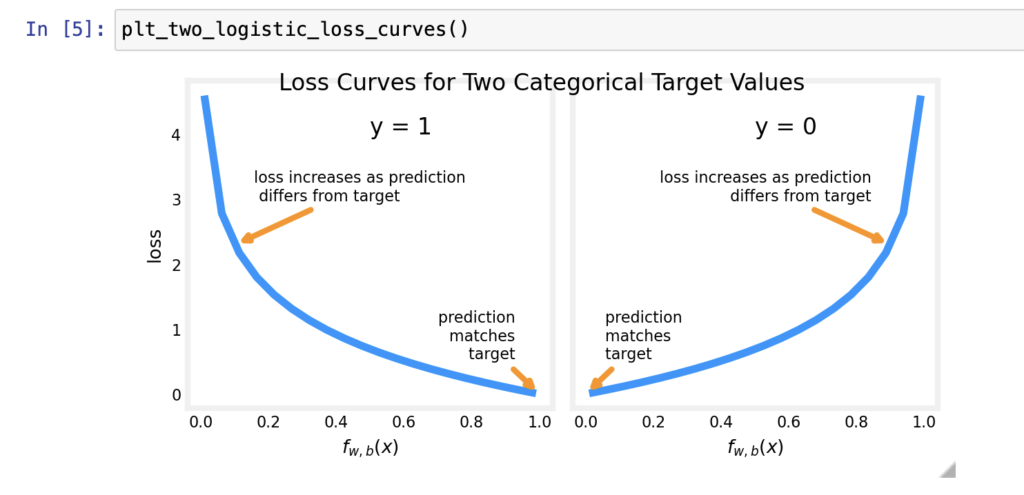
This particular cost function in above is derived from statistics using a statistical principle called maximum likelihood estimation (MLE).
Questions and Answers
- Why do we need loss function?
Logistic regression requires a cost function more suitable to its non-linear nature. This starts with a Loss function. - Why is the square error cost function not applicable to logistic regression?
- What is maximum likelihood?
- In logistic regression, "cost" and "loss" have distinct meanings. Which one applies to a single training example?
A: The term "loss" typically refers to the measure applied to a single training example, while "cost" refers to the average of the loss across the entire dataset or a batch of training examples.
Some thoughts of today
Honestly, it feels like it's getting tougher and tougher.
I can still get through the equations and derivations alright, it’s just that as I age, I feel like my brain is just not keeping up.
At the end of each video, Andrew always congratulates me with a big smile, saying I’ve mastered the content of the session.
But deep down, I really think what he's actually thinking is, "Ha, got you stumped again!"
However, to be fair, Andrew really does explain things superbly well.
I hope someday I can truly master this knowledge and use it effortlessly.
Fighting!
