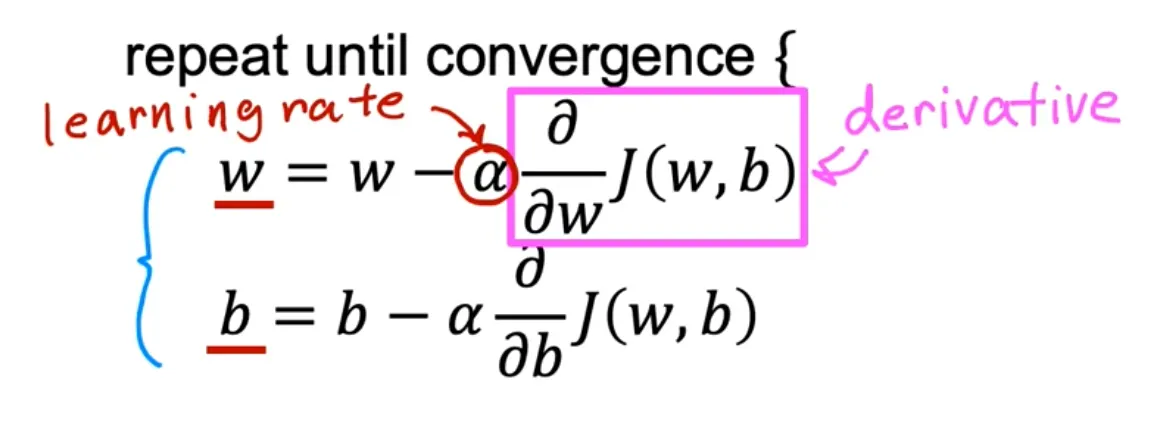
# Supervised Machine Learning – Day 2 & 3 - On My Way To Becoming A Machine Learning Person
Table of Contents
A brief introduction
Day 2 I was busy and managed only 15 mins for “Supervised Machine Learning” video + 15 mins watched But what is a neural network? | Chapter 1, Deep learning from 3blue1brown.
Day 3 I managed 30+ mins on “Supervised Machine Learning”, and some time spent on articles reading, like Parul Pandey’s Understanding the Mathematics behind Gradient Descent, it’s really good. I like math 😂
So this notes are mixed.
Notes
Implementing gradient descent
Notation
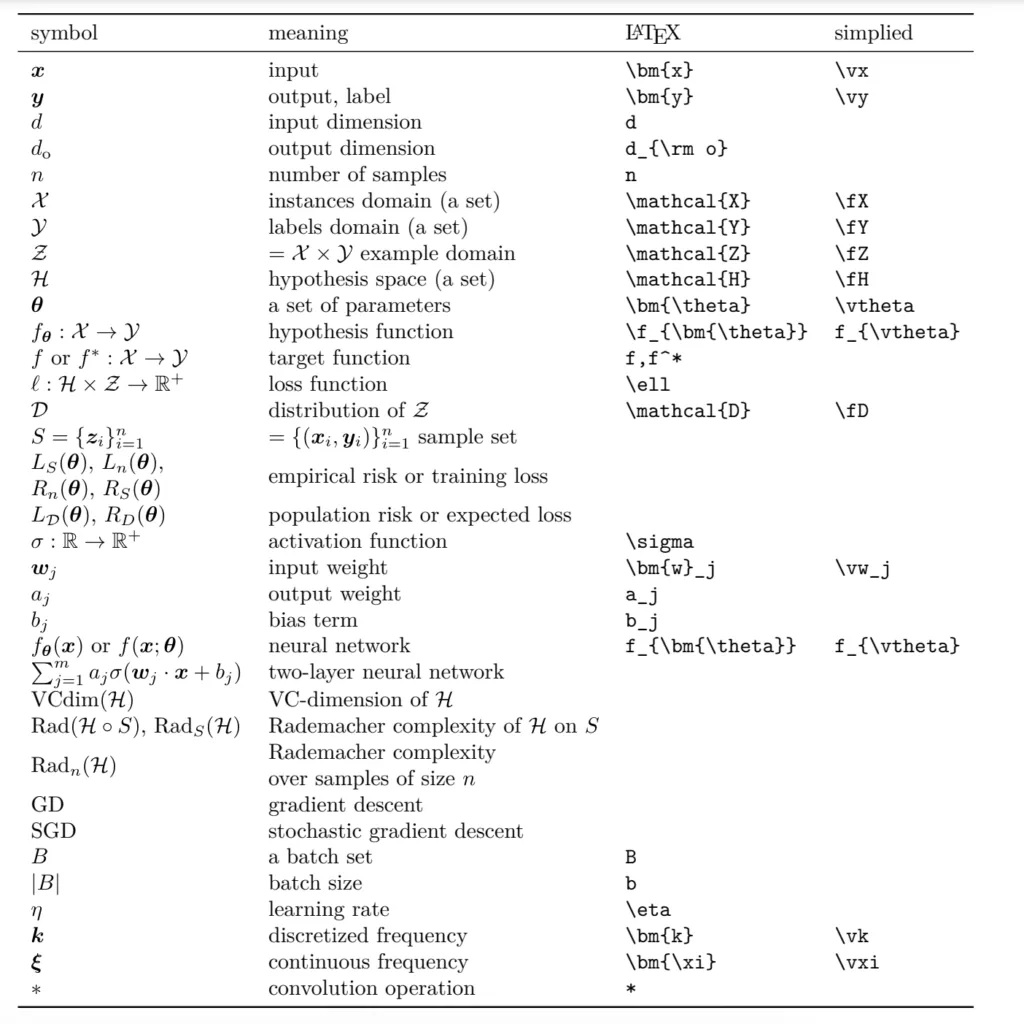
I was struggling in writting Latex for the formula, then found this table is useful (source is here):
Andrew said I don’t need to worry about the derivative and calculas at all, I trust him, next I dived into my bookcases and found out my advanced mathmatics books used in college, and spent 15 mins to review, yes, I don’t need.
Snapped two epic shots of my “Advanced Mathematics” book used in my college time to show off my killer skills in derivative and calculus - pretty sure I’ve unlocked Math Wizard status!


Reading online
Okay. Reading some online articles.
If we are able to compute the derivative of a function, we know in which direction to proceed to minimize it (for the cost function).
From Parul Pandey, Understanding the Mathematics behind Gradient Descent
Parul briefly introduced Power rule and Chain rule, fortunately, I still remember them learnt from colleage. I am so proud.
After reviewing various explanations of gradient descent, I truly appreciate Andrew’s straightforward and precise approach!
He was kiddish some times drawing a stick man walking down a hill step by step, suggesting that one might imagine flowers in the valley and clouds in the sky. This comfortable and engaging method made me forget I was in learning mode!
The hardest part still comes
But anyway, the hardest part still comes, I need to master this at the end:
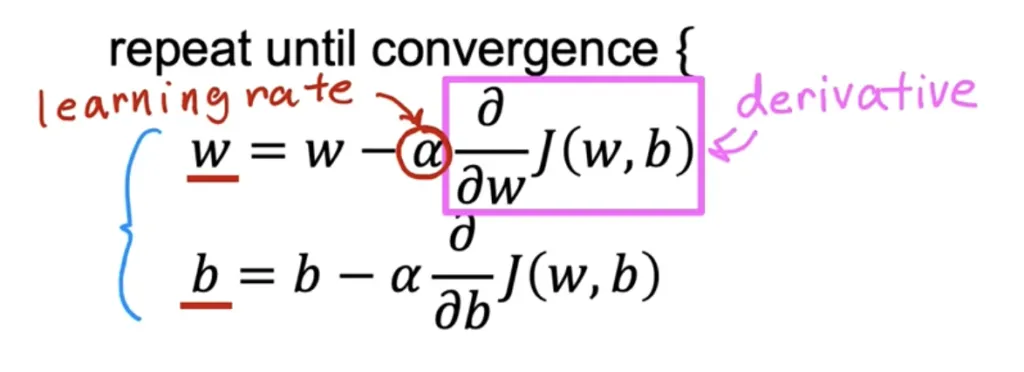
Learning Rate
If ⍺ is too small -> baby step, taking long time to get minimum.
If ⍺ is too big -> stride, may overshot, may never reach minimum. Fail to converge, even diverge.
What if w is near at the local minimum?
-
The derivative will become smaller.
-
The updated step will also become smaller
Above will result reaching minimum without decreasing learning rate.
At here, the conclusion came:
So that’s the gradient descent algorithm, you can use it to try to minimize any cost function J.
Not just the mean squared error cost function that we’re using for the new regression.
Tips:
-
Used derivative (partial derivative)
-
Needs to update w and b simultaneously. This requires to use a temp variable (Of course, it’s a standard practice in programing)
Finished Week 1’s course!
It’s a milestone to me!
I used 3 days (technically two days) finished the first week’s course!
I love ML! Let’s continue the momotum!
Terminology
| Term | Comments |
|---|---|
| Squared error cost function | |
| Local minimal | |
| Tangent line | Andrew introduced this when trying to show how derivative impact the cost. |
| Converge/Diverge | |
| Convex function | It has a single global minimum because of this bowl-shape. The technical term for this is that this cost function is a convex function. |
| Batch Gradient Descent | ”Batch”: Each step of gradient desent uses all the training examples. |